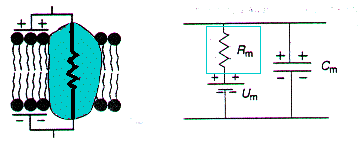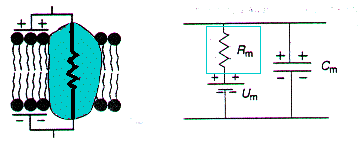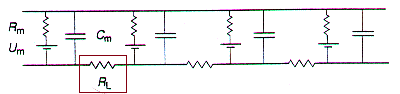|
Les protéines membranaires sont des molécules chargées électriquement et, comme tout élément porteur de charges, peuvent conduire un courant électrique. Cette propriété peut être schématisée par une conductance ou par une opposition au passage du courant, soit par une résistance (inverse de la conductance : R = 1/g). membranaire transversale. Le circuit électrique équivalent à la membrane neuronale correspond donc jusque là à celui d'un générateur de courant (pile) de 60 mV dont le pôle positif est orienté vers le compartiment extracellulaire et le pôle négatif vers l'intérieur de la cellule alimentant une résistance membranaire Rm. La valeur de cette résistance membranaire (Rm), directement fonction de la quantité de protéines incluses dans une portion de membrane, est très variable : de 102 à 104 W . cm2; ces valeurs correspondent à des conductances (g = 1/R) variant de 10-4 à 10-2 Siemens / cm2.
À l'inverse, la bicouche lipidique est constituée de phospholipides non conducteurs, donnant à la membrane des propriétés capacitives, qui peuvent être représentées par un condensateur (deux éléments conducteurs séparés par un isolant) de capacité Cm. Ce condensateur ne modifie pas la valeur de la ddp mais joue le rôle d'un "réservoir" de charges, qui absorbe les variations instantanées de ddp entre les deux faces de la membrane. La séparation des charges positives et négatives portées par le condensateur induit une ddp entre les deux éléments conducteurs telle que V (Volts) = Q (Coulombs) / Cm (Farads) où Q est la charge portée par les éléments conducteurs. La valeur de la capacité membranaire Cm varie peu d'un élément de membrane à l'autre; elle est en moyenne de 1 µF/cm2. |
| Ces propriétés électriques de la membrane neuronale ont des conséquences fonctionnelles.
Si l'on tient compte des propriétés résistives de la membrane neuronale (résistance transversale Rm), l'injection d'un courant I au travers de cette membrane (courant transmembranaire Im) fait apparaître, aux bornes de cette membrane, une tension Um telle que :
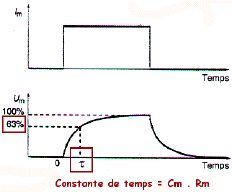
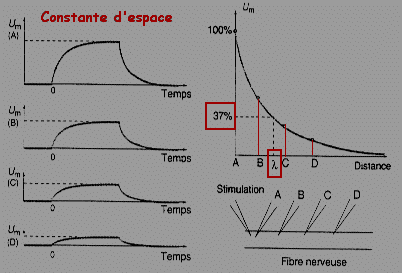
En réalité, si la variation du courant est rapide, la variation du potentiel de membrane suit une courbe exponentielle, du fait des propriétés capacitives (Cm) de la membrane. La résistance transversale Rm et la capacité Cm conjuguent leurs effets pour déterminer l'évolution dans le temps de l'installation de la tension Um aux bornes de la membrane. Le produit Rm . Cm est la constante de temps du circuit (t). Ce produit indique, en secondes, le temps nécessaire pour que la tension aux bornes de la membrane atteigne 63,2% de sa valeur maximum. |
|
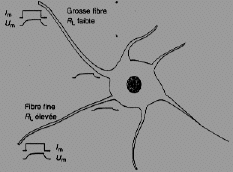
De par sa structure, la membrane neuronale est mauvaise conductrice. Une stimulation électrique de cette membrane est déformée comme dans un système résistif-capacitif (Rm - Cm) et ne se propage que sur de courtes distances liées aux diamètres des fibres (RL).
LES MÉCANISMES IONIQUES À L'ORIGINE DU POTENTIEL DE REPOS
Dans toutes les cellules, la répartition des ions de part et d'autre de la membrane est inégale. Les principaux ions libres rencontrés sont les ions Na+, K+, Ca2+ et Cl-. |
|
LA DISTRIBUTION DES IONS DE PART ET D'AUTRE D'UNE MEMBRANE PLASMIQUE OBÉIT À DEUX GRANDS PRINCIPES : L'ÉLECTRONEUTRALITÉ ET L'ÉQUILIBRE OSMOTIQUE |
|
Les solutions ioniques des milieux intra et extracellulaire doivent être électriquement neutre. Elles doivent chacune contenir autant d'anions (A-) que de cations (C+). C'est le principe de l'électroneutralité.

|
Milieu Extérieur |
[CATIONS]e = [ANIONS]e en mEq |
[Na]e + [K]e + 2 x [Ca]e = [Cl]e
140 + 5 + (2 x 1) = 147 |
|
Milieu Intérieur |
[CATIONS]i = [ANIONS]i en mEq |
[Na]i + [K]i + 2 x [Ca]i = [Cl]i + [P]i
14 + 140 + (2 x 10-4) = 14 + [P]i
[P]i = - 140 mEq | |
|
Le nombre de particules en solution situé de chaque côté de la membrane doit être le même, quelle que soit la charge de ces particules. C'est l'équilibre osmotique. En effet, si la pression osmotique des deux milieux n'est pas égale, il se produira des mouvements d'eau (du milieu le moins concentré vers le milieu le plus concentré) qui modifieront le volume cellulaire.
[IONS]e = [IONS]i en mOsm |
[Na]e + [K]e + [Ca]e + [Cl]e = [Na]i + [K]i + [Ca]i + [Cl]i + [P]i
140 + 5 + 1 + 147 = 14 + 140 + 10-4 + 14 + [P]i
[P]i = 125 mOsm Valence de P = - 140 / 125 = - 1,12 | |
|
L'EXISTENCE D'UN GRADIENT DE CONCENTRATION D'UN ION DE PART ET D'AUTRE D'UNE MEMBRANE PERMÉABLE À CET ION ENTRAÎNE LA FORMATION D'UN GRADIENT ÉLECTRIQUE |
|
Soit une membrane séparant deux compartiments 1 et 2, contenant des solutions ioniques isotoniques. Cette membrane est perméable à l'eau et aux cations (+) mais imperméable aux anions (-). La concentration en anions (-) et en cations (+) est plus élevée dans le compartiment 1 que dans le compartiment 2. |
A. Sous l'influence du gradient de concentration : [C+]1 > [C+]2, les cations, seuls diffusibles, vont passer du compartiment 1 vers le compartiment 2 (flèches noires). Ces cations, quittant le compartiment 1, libèrent les charges (-) des anions non diffusibles et créent un excédent de charges (+) dans le compartiment 2. Le travail fourni pour déplacer un ion le long de son gradient de concentration dépend :
de la constante des gaz parfaits R = 8.314 joules / mol./ °K
de la température absolue T° Kelvin = T° Celsius + 273
des concentrations dans chaque compartiment [C+]1 & [C+]2
tel que : W [ ] = R. T. ln [C+]2 / [C+]1
B. Le transfert des cations de 1 vers 2 a "polarisé" la membrane [1 : (-) - 2 : (+)] et crée un gradient électrostatique de 2 vers 1, qui tend à s'opposer à la fuite ionique né du gradient de concentration. Le travail électrostatique, s'opposant à la diffusion de l'ion dépend :
de la valence de l'ion Z
de la quantité d'électricité que représente un ion gramme F = Faraday = 96 500 coulombs
de la force électromotrice générée E
|
Le flux ionique né d'un gradient de concentration est autolimité par le champ électrique qu'il engendre.
Z. F. E. = R. T. ln [C+]2 / [C+]1
Eion (Volts) = R .T / Z . F . ln [C+]2 / [C+]1
ÉQUATION DE NERNST |
| ATTENTION !
Pour effectuer ces calculs, nous partons, à chaque fois, du principe que la membrane est perméable à un seul ion et imperméable aux autres. De plus, les valeurs calculées varient selon les cellules en fonction des concentrations ioniques des milieux extra- et intracellulaires comme de la température centrale de l'espèce (invertébrés ou mammifères ) à laquelle appartiennent les cellules étudiées.
Soit une membrane neuronale de mammifère :
T = 37°C = 37 + 273 = 310 °K
R . T / F = (8.314 . 310) / 96 500 = 0.026
ln = 2.3 log10
1 Volt = 1 000 millivolts (mV)
Si, par convention, le milieu extracellulaire est le milieu de référence et que nous prenions les valeurs des concentrations ioniques extra- ([ion]e) et intracellulaires ([ion]i) indiquées sur la figure :
Eion (mV) = [(1 000 x 0.026 x 2.3) / Z] log10 [ion]e / [ion]i = 60 / Z log10 [ion]e / [ion]i
| Potentiel d'équilibre des ions K+ |
EK = - 87 mV |
| Potentiel d'équilibre des ions Na+ |
ENa = + 60 mV |
| Potentiel d'équilibre des ions Ca2+ |
ECa = + 120 mV |
| Potentiel d'équilibre des ions Cl- |
ECl = - 61 mV |
PERMÉABILITÉ MEMBRANAIRE ET CANAUX IONIQUES : LES MÉCANISMES MEMBRANAIRES À L'ORIGINE DU POTENTIEL DE REPOS |
| Nous savons que, la couche bilipidique étant imperméable aux ions, les mouvements passifs des ions ne se font qu'au niveau de protéines transmembranaires spécialisées : les protéines-canaux dont la structure tridimensionnelle délimite un pore aqueux au travers duquel passent sélectivement certains ions. Elles assurent elles-mêmes le passage des ions à travers la membrane - elles sont aussi appelées canaux ioniques. |
1. LE GRADIENT ÉLECTROCHIMIQUE : Vm - Eion
Pour traverser la membrane, un ion est soumis à un gradient électrochimique (ou "driving-force" des anglo-saxons), qui s'exprime par la différence entre le potentiel de membrane (Vm) de la cellule et le potentiel d'équilibre de l'ion considéré (Eion). Le flux net d'une espèce ionique au travers de ses propres canaux est proportionnel à ce gradient électrochimique. |
POTENTIEL D'EQUILIBRE |
GRADIENT ELECTRO-CHIMIQUE |
FLUX NET |
| EK = - 87 mV |
Vm - EK = -60 - (-87) = + 27 mV |
SORTANT |
| ENa = + 60 mV |
Vm - ENa = -60 - (+60) = - 120 mV |
ENTRANT |
| ECa = + 120 mV |
Vm - ECa = -60 - (+120) = - 180 mV |
ENTRANT |
| ECl = - 61 mV |
Vm - ECl = -60 - (-61) = + 1 mV |
ÉQUILIBRE |
| Par convention, le flux net est positif quand un cation a tendance à sortir de la cellule et est négatif quand le cation a tendance à y entrer. | |
2. LA CONDUCTANCE IONIQUE MEMBRANAIRE
D'une manière générale, la conductance électrique (exprimée en Siemens, S) mesure la facilité avec laquelle un courant se déplace entre deux points : c'est l'inverse de la résistance (exprimée en ohms, W).
Dans le cas d'un canal ionique, la conductance caractérise la facilité avec laquelle les ions traversent le pore aqueux de la protéine-canal. |
|
La conductance de toute la membrane d'une cellule pour un ion (conductance ionique membranaire), gion, est proportionnelle à la conductance élémentaire d'un canal ionique : gion, mais aussi au nombre total de canaux de l'espèce ionique considérée dans la membrane : Nion et à la probabilité p0 pour que ces canaux soient à l'état ouvert :
|
|
La valeur de gion peut varier de 10 à 200 pS (1 picoSiemens, pS = 10-12 Siemens) selon le type de canal ionique. Notons que la plupart des canaux ioniques ne sont pas parfaitement sélectifs : la mesure de gion dépend donc des conditions expérimentales et, en particulier, de la présence d'autres ions. |
3. LES COURANTS IONIQUES
L'électrophysiologiste mesure des courants. L'intensité du courant (Iion, exprimé en Ampères : Coulombs.sec-1) traversant un canal ionique ou courant ionique élémentaire est égale à : |
Courant ionique membranaire (Iion) = gion (Vm - Eion)
ce qui n'est que la transposition de la loi d'Ohm (V = RI donc I = g V) à un gradient électrochimique |
4. LA MEMBRANE NEURONALE EST PERMÉABLE À PLUSIEURS IONS : DÉTERMINATION DU POTENTIEL DE REPOS
On pensait, au début (J. Bernstein, 1902), que la membrane neuronale était sélectivement perméable aux ions K+. Des études plus récentes ont pu montrer que la membrane neuronale au repos est perméable, à la fois, aux ions K+ et Na+. Il apparaît simplement, qu'au repos, la conductance membranaire des ions K+ (gK) est plus grande que celle des ions Na+ (gNa). |
|
Supposons une cellule dont la membrane comporte, à la fois, des canaux K+ et Na+ ouverts. Nous savons que cette cellule dispose de mécanismes de transport actif (pompe Na+/K+/ATPase) qui permettent de maintenir les concentrations des ions K+ et Na+, de part et d'autre de la membrane, constantes. Les potentiels d'équilibre des ions K+ (EK) et Na+ (ENa) restent donc constants. Le potentiel de membrane (Vm), qui va s'établir, est donc intermédiaire entre les potentiels d'équilibre des deux ions, soit entre EK (-87 mV) et ENa (+ 60 mV).
Le potentiel de membrane de la cellule (Vm) atteindra un état stable quand le flux net des charges (K+ & Na+) passant à travers la membrane sera nul, soit, en termes de courants ioniques, quand INa + IK = 0.
Or nous savons que :
IK = gK (Vm - EK)
INa = gNa (Vm - ENa)
Quand :
gK (Vm - EK) + gNa (Vm - ENa) = 0
Vm = (gK . EK + gNa . ENa) / (gK + gNa)
La valeur du potentiel de membrane dépend de la conductance relative des deux ions, leurs potentiels d'équilibre restant constants, et donc du rapport gNa / gK
Si a = gNa/gK :
Vm = (EK + a. ENa) / 1 + a |
|
Dans notre exemple, où Vm = -60 mV, EK = -87 mV et ENa = + 60 mV, a = 0.2, ce qui signifie que la conductance des ions K+ est 5 fois plus grande que celle des ions Na+ soit : gK = 5. gNa.
Dans la majorité des cellules au repos, il y a beaucoup plus de canaux K+ que de canaux Na+ ouverts. Mais, le courant sortant potassique n'est cependant pas 5 fois plus important que le courant entrant sodique car le gradient électrochimique potassique (Vm - EK = + 27 mV) est beaucoup moins important que le gradient électrochimique sodique (Vm - ENa = - 120 mV). En fait, 2 ions K+ sortent de la cellule quand 3 ions Na+ y entrent. La cellule nerveuse aurait donc tendance à se vider de son K+ et à se remplir de Na+ si un système de transport actif, et donc consommateur d'énergie, ne venait rétablir l'équilibre en expulsant 3 ions Na+ contre l'entrée de 2 ions K+. |
5. LA POMPE Na / K / ATPase MAINTIENT LES CONCENTRATIONS IONIQUES EN K+ ET Na+ INTRA- ET EXTRACELLULAIRE CONSTANTES |
|
Une expérience, aujourd'hui classique, utilisant du Na+ radioactif, montre que du Na+ est perpétuellement rejeté de la cellule contre son gradient électrochimique. Un axone géant de calmar est incubé quelques minutes dans du liquide de Ringer contenant du Na+ radioactif : le Na+ radioactif pénètre par diffusion passive dans l'axone, en fonction du gradient électrochimique du Na+.
- L'axone est ensuite placé dans un milieu normal : le milieu s'enrichit progressivement en Na+ radioactif, qui ne peut provenir que de l'axone (sortie de Na+), et ce par un mécanisme de transport actif qui s'oppose au gradient électrochimique du Na+.
- Si l'axone empli de Na+ radioactif est plongé dans un milieu contenant du dinitrophénol (DNP), soit un inhibiteur du métabolisme cellulaire, le flux sortant de Na+ s'arrête, et ce de façon réversible : la sortie de Na+ est donc bien un phénomène actif lié à des processus métaboliques. L'ATP étant la plaque tournante du métabolisme énergétique dans la cellule, l'adjonction d'ATP au milieu contenant du DNP provoque bien une reprise de la sortie du Na+, dont l'importance est proportionnelle à la quantité d'ATP ajoutée.
- Si l'axone empli de Na+ radioactif est plongé dans un milieu dépourvu d'ions K+, le flux sortant de Na+ s'arrête également : la sortie de Na+ dépend de la présence d'ions K+ dans le milieu ([K+]e).
- En modifiant les concentrations de Na+ intracellulaire, on peut également montrer que la sortie de Na+ de l'axone est fonction de la concentration intracellulaire en Na+ ([Na+]i).
Le modèle, encore hypothétique, de la pompe Na+/K+/ATPase postule l'existence d'une protéine transmembranaire dont la partie externe aurait 3 sites de liaison : 2 sites pour les ions K+ et un site pour l'ouabaïne (bloquant de la pompe). - la partie interne de la protéine, située vers le cytoplasme de la cellule, porterait le site de liaison de l'ATP et 3 sites de liaison pour les ions Na+. Chaque fois que 3 ions Na+ sont expulsés de la cellule, 2 ions K+ entrent dans la cellule. |
 |
| |